Fibonacci Series

This is very popular basic question often asked from beginners to check their recursive algorithm knowledge. This it will lead to some performance question, not much hard , but to how to improve, with testing memorization concept.

Fibonacci series is a number series where each number is built with the sum of the following two numbers.


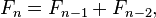
1, 1, 2,3, 5, 8, 13 ......

Or
 0, 1, 1, 2, 3, 5, 8, 13 .....

This can be done using recursive algorithm as below.

------------------------------------------------------------------------
public static Integer fibR(Integer number) {

if (number == 1 || number == 2) {
return 1;
}
return fibR(number - 1) + fibR(number - 2);
}

----------------------------------------------------------------------------

This has some small issue, where recursion will have duplicate calls to calculate same fibonacci value.


eg: If we calculate Fibonacci(5) , or value of Fibonacci series at 5 th position, we need Fibonacci values from Fibonacci(0)  to Fibonacci(5)
But with recursive way , except for Fibonacci(5) , all values are called repetitively. This is a waste.

So what we need to do. There the question of memorization will come to action.
That is, if we can have the memory of the values we have already calculated, then we can reuse them, without recalculating.

So we need to functionality to be made.
1. Keep the calculated Fibonacci values in memory
2. Before calculating new value, check whether value is calculated and need to have a retrieving mechanism of stored value.

Note : recursive algorithm is calling all the nodes, until get the leaf node
(  depending on your definition of Fibonacci series , series will defines as fib(0) , fib(1), fib(2).... or fib(1), fib(2), fib(3)...   )
So in both cases leaf nodes will be fib(0) , fib(1),  or fib(1), fib(2) respectively.
calculation happens from bottom to top after calling to create each node.
So Recursive algorithm is bottom up.

Next when come to memorization , I have create in top down approach.

--------------------------------------------------------------------------------------------------------------------------

public static Integer fibM(Integer number) {
HashMap cache = new HashMap();
cache.put(1, 1);
cache.put(2, 1);

if (number == 1 || number == 2) {
return 1;
}

// for memorization, we go from top to bottom - fib(1) to fib(n)
for (Integer i = 3; i <= number; i++) {
cache.put(i, cache.get(i - 1) + cache.get(i - 2));
}

return cache.get(number);
}

--------------------------------------------------------------------------------------------------------------------------

I have used a HashMap to cache the calculated values and finally return the Fibonacci  value.